- Geometria -
De Pitágoras? Mas a "gema" não era egípcia? Semelhante ao diamante, que antes da lapidação não tem brilho, o grande teorema surgiu há cerca de 4000 anos no Egito. Mas foi o matemático grego que imprimiu sua marcante "lapidação", há cerca de 2500 anos.
Para legitimar sua autenticidade, muitos estudiosos inclusive Leonardo da Vinci, o submeteram à rigorosas provas matemáticas ao longo de sua história.
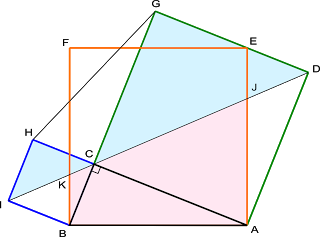
Aqui, o filósofo "lapida"uma elegante configuração geométrica, que constitui prova matemática do teorema de Pitágoras.
Acompanhe a construção, em seus passos conclusivos.
Passo 1
Considerando um triângulo retângulo ABC qualquer.
Passo 2
a² + b² = c²
O Teorema de Pitágoras afirma que
a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Passo 3
Rebata o quadrado da hipotenusa sobre
o triângulo ABC e os quadrados dos catetos.
Assim o triângulo retângulo se reproduzirá
crongruentemente em EDA.
o triângulo ABC e os quadrados dos catetos.
Assim o triângulo retângulo se reproduzirá
crongruentemente em EDA.
Passo 4
Trace a bissetriz ID, que divide exatamente ao meio os quadrados
dos catetos e o da hipotenusa, surgindo o polígono IDAB.
dos catetos e o da hipotenusa, surgindo o polígono IDAB.
Passo 5
Trace o segmento HG. O triângulo retângulo
volta a reproduzir-se congruentemente em HGC,
e surge o polígono HGDI que sendo congruente
a IDAB por simetria ao eixo ID, têm área igual.
volta a reproduzir-se congruentemente em HGC,
e surge o polígono HGDI que sendo congruente
a IDAB por simetria ao eixo ID, têm área igual.
Passo 6
Removidos do polígono IDAB, os triângulos IKB e JDA,
e do polígono HGDI, o triângulo HGC,
ficaram os triângulos IHC e CGD, e o polígono KJAB,
que representam exatamente metade dos quadrados dos catetos
e metade do quadrado da hipotenusa.
e do polígono HGDI, o triângulo HGC,
ficaram os triângulos IHC e CGD, e o polígono KJAB,
que representam exatamente metade dos quadrados dos catetos
e metade do quadrado da hipotenusa.
Passo 7
Os triângulos HGC, EDA e ABC são congruentes.
Os quadrados HCBI e EDML são congruentes.
IB é paralelo a ED, e por simetria, KB é congruente a EJ,
e IK congruente a JD. Logo os triângulos IKB e EDJ são congruentes.
Os quadrados HCBI e EDML são congruentes.
IB é paralelo a ED, e por simetria, KB é congruente a EJ,
e IK congruente a JD. Logo os triângulos IKB e EDJ são congruentes.
Passo 8
Sendo IKB e EDJ congruentes, a soma das áreas
de IKB e JDA é igual a área do triângulo HGC.
de IKB e JDA é igual a área do triângulo HGC.
Passo 9
Divididos pela bissetriz ID, os quadrados dos catetos
e o da hipotenusa resultam respectivamente
nos triângulos IHC e CGD e no trapézio KJAB.
Sendo a soma das áreas dos triângulos igual a área
do trapézio, efetiva-se essa construção geométrica
que constitui prova matemática do teorema de Pitágoras.
e o da hipotenusa resultam respectivamente
nos triângulos IHC e CGD e no trapézio KJAB.
Sendo a soma das áreas dos triângulos igual a área
do trapézio, efetiva-se essa construção geométrica
que constitui prova matemática do teorema de Pitágoras.








Vera Henriques,
ResponderExcluirSim a ostra é egípcia, mas o diamante é eterno...
Pitágoras não estaria simbolizando o saber da mineralogia simbólica indiana que revela o diamante maduro a partir do embrião do cristal? Então, ... por que, não dizer... o diamante de Pitágoras?
ANGELA REIS
ResponderExcluirCONCLUI-SE QUE A LAPIDAÇÃO REFERENTE A UMA DETERMINADA COISA,QUE PARECIA PELA SUA APARÊNCIA NÃO SER IMPORTANTE , APÓS DELICADAMENTE PASSADO PELO UM PROCESSO DE CUIDADOS, MOSTROU-SE EXUBERANTE AOS OLHOS DE QUEM A LAPIDOU!COM SENTIDOS DE SIGNIFICADOS DE VÁRIAS FORMAS ESPECIAIS E DE MUITA IMPORTÂNCIA . AO LONGO DO TEMPO TORNOU-SE MUITO VALOROSA .ESTA OBRA QUE JÁ EXISTIA MAS NÃO ERA PERCEBIDA,TENDO SEGUIMENTO DE ENTENDIMENTOS DIFERENCIADOS DE REALIDADE VISUALIZADAS.
Amorim:
ResponderExcluirComo toda lapidação depende o ourives que a executa, os nossos aprendizes dessa arte poderiam melhor entendê-la se os mestres, usando por exemplo o Passo 2 da explicação, explicassem que um número, quando elevado ao quadrado, não é a simples operação aritmética de multiplicação dele por si mesmo, mas que se os dispusermos geometricamente, perceberemos que um grande quadrado de 3 é formado por nove idênticos quadrados menores no interior.
Para demonstrar isso em sala de aula é muito fácil. Se o piso da sala é formado por lajotas quadradas, basta mandar o aluno olhar para o chão, e será fácil explicar que três quadrados de comprimento por três quadrados de largura formam um grande quadrado com 9 unidades.
Faz-se o mesmo com outro quadrado de quatro, que resultará em 16 unidades idênticas, e teremos, de ambos, os dois catetos formados pelas unidades internas idênticas.
Basta usar a mesma unidade dos catetos na hipotenusa e obteremos um quadrado grande formado por 25 unidades.
Essa explicação, retirada do livro O Homem Que Calculava (Malba Tahan), é usada pela minha esposa, professora no Ensino Fundamental da rede municipal já no aprendizado da Taboada sem qualquer dificuldade no aprendizado das crianças.
O que prova que a Geometria é a Mãe da Matemática, e não o contrário, usualmente sugerido.